Schema d'Integrazione
Nell'analisi dinamica non lineare, si deve utilizzare uno schema di integrazione numerica diretta per poter risolvere il sistema di equazioni del moto [es. Clough and Penzien, 1993; Chopra, 1995]. In SeismoBuild questa integrazione può essere condotta con due differenti algoritmi impliciti di integrazione: lo schema di integrazione di Newmark [Newmark, 1959] e l'algoritmo di integrazione di Hilber-Hughes-Taylor [Hilber et al., 1977]. Quest'ultimo è l'opzione di default.
Schema d'integrazione di Newmark
Lo schema d'integrazione di Newmark richiede la definizione di due parametri; beta (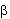
) e gamma (
). Si può ottenere una stabilità non condizionata, indipendentemente dal passo di tempo utilizzato, per valori di 
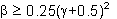. In aggiunta, se si utilizza = 0.5, lo schema d'integrazione si riduce alla ben nota regola trapezoidale non dissipativa, in cui non si introduce smorzamento numerico, condizione che può essere vantaggiosa in molte applicazioni. I valori di default sono quindi 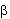= 0.25 e = 0.5.
Schema d'integrazione di Hilber-Hughes-Taylor
L'algoritmo di Hilber-Hughes-Taylor, richiede invece la definizione di un parametro addizionale alfa (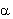
) usato per controllare il livello di dissipazione numerica. Quest'ultima può giocare un ruolo benefico nelle analisi dinamiche, soprattutto attraverso la riduzione del contributo dei modi spuri più elevati alla soluzione (che tipicamente si manifestano nella forma di picchi molto alti di breve durata), incrementando in questo modo sia l'accuratezza dei risultati che la stabilità numerica dell'analisi. In accordo con gli autori [Hilber et al., 1977], e come confermato in altri studi [es. Broderick et al., 1994], soluzioni ottimali in termini di accuratezza della soluzione, stabilità numerica e smorzamento numerico sono ottenute per valori di 
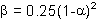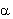e = 0.5 - , con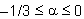 
. In SeismoStruct, i valori predefiniti sono 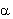= -0.1, 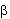= 0.3025 e = 0.6.
Nota: Per ulteriori approfondimenti e chiarimenti su argomenti quali le procedure di soluzione al passo, i metodi impliciti ed espliciti, le condizioni di stabilità, lo smorzamento numerico e così via, si raccomanda di riferirsi alla letteratura disponibile, come i lavori di Clough and Penzien [1993], Cook et al. [1988] e Hughes [1987], per citarne alcuni.